正直、この定理はあまりにも有名です。
数学が好きな人なら誰もが聞いたことがあるし、
「もう知ってるよ!」という方もいるかもしれません。
でも、それでも僕は紹介したいんです(笑)
なぜなら、これは「数式の話」ではなく、
**人間の情熱・執念・夢が350年以上も受け継がれていく“物語”**だからです。
しかもこの定理を残したピエール・ド・フェルマーは、
プロの数学者ではありません。
彼の本業は裁判官で、数学はあくまで“趣味”だったんです。
つまり、フェルマーはアマチュア数学者でした。
そんな人物が書き残したたった一行が、
世界中の天才たちを何百年も翻弄することになるなんて――
もうそれだけでロマンを感じます。
◆ すべては一冊の数学書の余白から
フェルマーは、生涯にわたって多くの数学書を読み、
その余白に自分の考えを書き込むのが習慣でした。
彼の死後、息子のクレマン=サミュエルが蔵書を整理していたとき、
一冊の余白に、こんな言葉が書かれているのを発見します。
「私はこの命題の驚くべき証明を見つけた。
しかし、この余白はそれを書くには狭すぎる。」
その命題とはこうです。
n が 2 より大きい整数のとき、
xⁿ + yⁿ = zⁿ を満たす自然数(x, y, z)は存在しない。
n=2、つまりピタゴラスの定理には無数の解があります。
しかし n=3 以上になると、整数解は一つも存在しないというのです。
フェルマーはそう主張し、
「証明はあるけれどここには書けない」とだけ残しました。
そしてこの一文が、350年に及ぶ数学者たちの戦いを生むことになります。
◆ 悪魔の定理――解けそうで解けない
フェルマーの最終定理は、短くて美しい命題です。
でも、証明しようとすると、すぐに底の見えない深みに落ちていきます。
解けそうで、解けない。
わかりそうで、全然わからない。
それはまるで人の理性を試す“悪魔の証明”のようでした。
証明しようと近づくたびに、新しい壁が現れる。
真実が見えたと思った瞬間、霧のように消える。
この「あと一歩なのに届かない」という感覚が、
数学者たちの心を強烈に惹きつけました。
◆ 挑み続けた英雄たち
● レオンハルト・オイラー
“数学の王”と呼ばれた天才。
n=3 の場合を証明し、フェルマーの主張に一歩近づきました。
それでも完全な証明には至らず、
**「天才一人では倒せない敵」**であることを示しました。
オイラーはもっと紹介したいのでまた別の記事で紹介しますね😁
● ガブリエル・ラメ
「証明できた!」と宣言し、ヨーロッパ中が歓喜しました。
しかし数日後、その証明に致命的な欠陥があることが判明。
喜びは一瞬で絶望に変わりました。
**フェルマーの定理は、手が届いたと思った瞬間に遠ざかる“悪魔の定理”**でした。
● ソフィー・ジェルマン
女性が数学を学ぶことさえ難しかった時代、
彼女は男性名を使って論文を提出しました。
夜な夜なロウソクの灯りの下で、数式と向き合い続けたのです。
彼女の独自の考えは、後に「ソフィー・ジェルマンの方法」として
多くの数学者の手がかりとなりました。
フェルマーの定理は、ただの数式の問題ではなかった。
「情熱と信念」が、どんな壁よりも強いことを示した証だったのです。
● エルンスト・クンマー
理想数という新しい概念を生み出し、証明に大きく迫った数学者。
しかし「不規則素数」という思いがけない壁に阻まれ、
あと一歩のところで完成には至りませんでした。
それでも彼の研究は失敗ではなく、
現代数学の土台となり、
後のワイルズによる最終的な証明への道を作りました。
◆ 一人の少年が見た夢
イギリスの少年アンドリュー・ワイルズ。
10歳のころ、図書館でフェルマーの最終定理を紹介した本を読み、
心の中で決めました。
「僕がこの定理を証明する。」
その夢は、大人になっても消えませんでした。
やがて彼は数学者となり、
「谷山・志村予想」という研究が
フェルマーの最終定理に深く関係していると知ります。
そして、静かに決意しました。
「今なら、いける。」
◆ 七年間の沈黙
ワイルズは誰にも言わず、
7年間ひとりで研究を続けました。
同僚にも、学生にも、家族にも秘密。
夜遅くまで研究室にこもり、
紙の山と数式に囲まれながら、ただひたすら挑み続けました。
「子どもの頃の自分との約束を果たすために。」
◆ そして1993年、奇跡の瞬間が訪れる
ワイルズは、ついに証明を発表します。
世界中の数学者が祝福し、ニュースでも大きく報じられました。
「350年の謎がついに解けた」と。
しかし――数か月後。
論文の査読で、証明に致命的な穴が見つかります。
世界が一転して沈黙しました。
◆ 絶望の中の再挑戦
ワイルズは諦めませんでした。
何度も書き直し、何度も壁にぶつかりながら、
静かな絶望の中で、ふと一つの“つながり”に気づきます。
過去の研究と新しい理論が、思いがけない形で結びついた瞬間でした。
そして数日後、証明は完成。
1995年、正式に「フェルマーの最終定理は証明された」と認められます。
少年の頃の夢が、30年以上の時を経て現実になった瞬間でした。
◆ 僕がこの話を好きな理由
正直、証明の中身は全く理解できません(笑)
でも、僕がこの定理を好きなのは、
これは数学の話じゃなくて**「人間の夢と情熱の話」**だからです。
フェルマーは趣味で残した。
オイラーやソフィーは命を削って挑んだ。
そしてワイルズは少年の夢を現実にした。
結果よりも、そこに至るまでの“挑戦の軌跡”こそが、美しいと思うんです。
◆ 最後に:夢は、追い続ける人の前に現れる
フェルマーが残したたった一行は、
もしかすると数学というより「人生」への問いかけだったのかもしれません。
「私は証明を見つけた。」
彼のその言葉は、
350年後に、一人の少年の心を動かし、
そして人類の夢を叶えました。
夢は、叶うかどうかではなく、
追い続けることにこそ意味がある。
そして本気で追い続けた人の前にだけ、
“扉の向こう側”が現れるのだと思います。
✏️まとめ
- フェルマーはアマチュア数学者だった
- 息子が整理した蔵書の余白から「伝説の一文」が見つかった
- 350年間、無数の天才が挑み、倒れ、それでも前へ進めた
- 最後に証明したのは、一人の少年が見た夢だった
僕はこの話を思い返すたびに、
「結果がすぐに出なくても、夢を持ち続けることは無駄じゃない」と感じます。
たとえ時間がかかっても、自分の“フェルマーの定理”を探して、
少しずつ前へ進んでいけたらと思います。
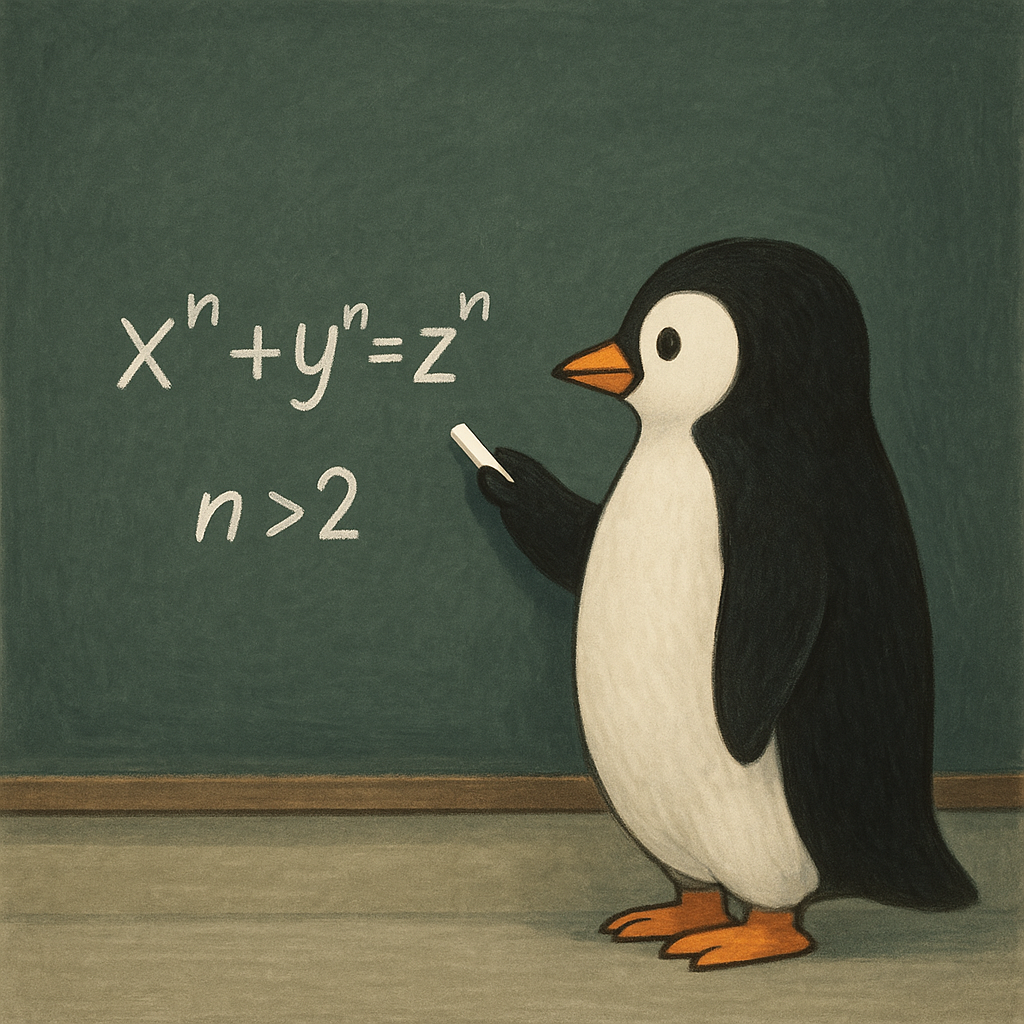
コメント